阪神・淡路大震災

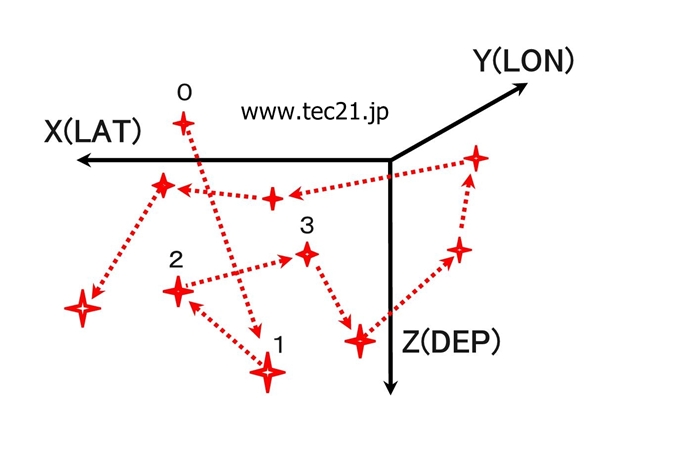
地殻の応力変化が起こすこれら地震の発生(星印)を、仮想粒子の出現とみなすと、地震発生の変化が残す痕跡（軌跡）は、仮想粒子が出現する度、その粒子の位置を直線で連結した軌跡とみなせる。

図3ｃでは、震源要素時系列ｄ（ｃ、ｍ）を２５イベントで移動平均したD(c,m)とその差分間隔ｓで２次差分を取ったA(c,m)は、最新時刻ｍ（ｍ＝６４０）からの時間遅れはない。一方、物理的ウエーブレットで観察した図９aには、時系列ｄ（ｃ、ｍ）、変位D(c,t)、加速度A(c,t)の間には時間遅れが生じる。加速度A(c,ｔ)は、ｔ＝ｍ－ｓ－Δｔ/2だけ遅れる。この加速度A(c,t)は、変位D(c,t)に作用しているが、加速度を算出するには、図８ｂのA1から得る変位D(c,t+s)を必要とする。従って、この変位D(c,t+s)は、LAT、LON、DEP、INT行に赤色表示されていてｍからΔｔ/2だけ遅れる。変位検出ウエーブレットの中央の時刻は、離散データｄ（ｃ,ｍ）の２５イベントの中央値となるので、Δｔ/2は、１２イベントとなる。従って加速度A(c,t)のｍからの遅れは、４７イベントとなる。図９aの他のグラフ表示方法は、図３ｃと、全て、同じである。

図3ｄの震源要素時系列ｄ（ｃ、ｍ）を２５イベントで移動平均したD(c,m)とその差分間隔ｓで２次差分を取ったA(c,m)とには、最新時刻ｍ（ｍ＝１０８０）からの時間遅れは、無い。一方、物理的ウエーブレットで観察した図９ｂには、時系列ｄ（ｃ、ｍ）、変位D(c,t)、加速度A(c,t)の間には時間遅れが生じる。加速度A(c,ｔ)は、ｔ＝ｍ－ｓ－Δｔ/2だけ遅れる。この加速度A(c,t)は、変位D(c,t)に作用しているが、加速度を算出するには、図８ｂのA1から得る変位D(c,t+s)を必要とする。従って、この変位D(c,t+s)は、LAT、LON、DEP、INT行に赤色表示されていてｍからΔｔ/2だけ遅れる。変位検出ウエーブレットの中央の時刻は、離散データｄ（ｃ,ｍ）の２５イベントの中央値となるので、Δｔ/2は、１２イベントとなる。従って加速度A(c,t)のｍからの遅れは、４７イベントとなる。図９ｂの他のグラフ表示方法は、図３ｄと、全て、同じである。

時間tを横軸に、加速度を縦軸に取り、A(INT,t)を実線、A(DEP,t)を破線、A(MAG,t)を実線として、描く。ただし縦軸は、上側がマイナス(負)、下側がプラス(正)領域となる。先ず、CQKは、略、2sの周期で変動していた加速度A(DEP,t)の周期が、時刻ta0付近から、A(INT,t)の周期より長くなり始める。そして、時刻ta1で、A(DEP,t)とA(INT,t)とが逆位相となり反転が生じる。反転時、A(INT,t)は、正の方向(INTを増加させる方向)に振幅のピーク値、A(DEP,t)は、負の方向(DEPを減少させる方向)に振幅のピーク値を取り、A(MAG,t)は、負の方向(マグニチュードを減少させる方向)に振幅のピーク値を取る。このCQKの大地震発生の時刻は、t軸上へ記した上向きの破線矢印の箇所で、A(INT,t)が、半周期後に、反転し、振幅の逆のピークに到達した時刻ta2である。CQTは、略、2sの周期で変動していた加速度A(INT,t)の周期が、時刻ta0付近から、CQKとは逆に、A(INT,t)の周期より長くなり始め、時刻ta1で、A(DEP,t)とA(INT,t)とが逆位相となり反転が生じる。反転時、A(INT,t)は、負の方向(INTを減少させる方向)に振幅のピーク値、A(DEP,t)は、正の方向(DEPを増加させる方向)に振幅のピーク値を取り、A(MAG,t)は、先のCQKと同様に、負の方向(マグニチュードを減少させる方向)に振幅のピーク値を取る。このCQTの大地震が発生するのは、t軸上へ記した上向き破線矢印の箇所の時刻ta2である。

図９ｄの遅れ時間は、差分間隔を取ったｓとなる。又、ｓだけ進んだ変位D(c,t+s)は、最新の時系列ｄ（ｃ、ｍ）を与える時刻ｍからΔｔ/2だけ遅れる。図９ｃに示した、加速度、A(c,ｔ)のCQKとCQT予兆の関係は、数式（2）の関係から、変位D(c,t)の関係に変換できる。

CQKDは、M7.2 兵庫県南部地震のタイプで、CQTDは、M7.2鳥取県西部地震のタイプの予兆である。

左側の模式図のＭ7.2の兵庫県南部地震等のCQK予兆検出時、地殻表面から深い個所で、M4地震が多発している。D(DEP,t)、D(INT,t)、D(MAG,t)は周期変動しているので、その半周期後、CQK予兆検出時の地震発生の状態から反転し、地殻表面から浅い個所で、M3.8地震が、時々発生している状態となる。深い個所から浅い個所への反転直後に、CQK予兆の大地震が、発生するので、この反転に伴う震源の深さD(DEP,t)の変化量に相当する応力変化が、CQK予兆の大地震の断層運動を起こす地殻の応力変化を誘発する。右側の模式図は、CQT型のM7.2の鳥取県西部地震等の場合である。大地震のCQT予兆検出時、地殻表面から浅い個所で、M4地震が時々発生している。D(DEP,t)、D(INT,t)、D(MAG,t)は周期変動しているので、その半周期後、CQT予兆検出時の地震発生の状態から反転し、深いい個所で、M3.8地震が、多発している。この反転直後に、CQT予兆の大地震が、発生する。

図７：地震発生の新たな概念

地震発生は仮想粒子の出現

例えば、中国・四国・近畿地方の4度×5度のメッシュを対象領域として選択する。気象庁一元化カタログと気象庁カタログから、その小さな領域内に発生した地震で、深発地震を除き、マグニチュード(Ｍ)が、Ｍ≧Ｍｃ(Ｍｃ=3.5)で選択される地震のみ抽出する。そして、これら地震の震源(緯度－LAT、経度－LON、深さ－DEP)を、地震が発生した順に辿り、その領域(3次元空間)に痕跡(軌跡)を描く。図７に、その3次元空間を表示する。ｘ軸を「LAT」、ｙ軸を「LON」、ｚ軸を「DEP」とすると、x-y平面が、地表面となり、ｚ軸が、地殻の深さとなる。地殻内の星印が、発生した地震で、星印を連結した折れ線(矢印の連結)が、地震が描いた軌跡となる。星印の大小は、地震のＭの大小を表す。地殻の応力変化が起こすこれら地震の発生(星印)を、仮想粒子の出現とみなすと、この軌跡は、仮想粒子が出現する度、その粒子の位置を直線で連結した軌跡となる。

図７に示した地震発生の痕跡は、丁度、液体中に浮遊している粒子が、ブラウン運動して描くジグザグした軌跡の様になる。浮遊粒子の運動軌跡は、所定の等間隔時間で、運動している粒子の位置を観測し、その位置を直線で連結して得る。地震発生の場合、震源時(地震の発生時刻)が、仮想粒子（地震）を観測した時刻tとなるが、その観測時刻tと粒子の出現順番を示す整数値ｊとの関係は一意的なので、整数値ｊを観測時刻とする。図７の「x-y-z空間」に、その出現時刻の一例を、0、1、2、3、として、発生した地震(星印)の横に、付記してある。

その仮想粒子の観測値は、３次元空間の位置情報に、地殻の応力変化の情報とマグニチュードとを加える事ができる。マグニチュードは、MAGもしくはMと定義する。応力変化は、前述した様に、地震の発生時刻の差である発生間隔時間(INT)に出現すると仮定できるので、INTをその応力変化の観測値とする。これら観測値が、(LAT、LON、DEP、INT、MAG)からなる５つの震源要素ｃとなる。従って、仮想粒子の運動は、3次元から5次元へと拡張した観測空間で記述できる。観測空間の次元数は、更に、追加できる。例えば、地震の発生は断層の破壊運動なので、断層面の向き、傾き、すべり方向等の地震の破壊メカニズム要素も観測値に加える事ができる [13, 14]。この様に拡張した空間に描いた軌跡の各座標軸成分が、地震の各要素の時系列データｄ（ｃ、ｊ）となり、地震の発生順番を示す整数値ｊが、各時系列に共通な時間となる。整数値のｊを時間とする事は、自然科学、工学等における情報や現象を時系列化する際、古くから頻繁に用いられている概念である。従って、時刻jで発生した地震が観測空間に描く軌跡は、時刻ｊで観測された仮想粒子が、その観測空間に描く運動軌跡と同等に取り扱う事ができるので、その粒子運動の位置、速度、加速度を用いて、地震の発生の変化を記述できる [14]。しかし、粒子が、ランダムでジグザグな運動をするので、その速度、加速度を求める微分操作は、ジグザグする箇所で、不可能となる。しかも、ランダム運動している粒子は、突如、決定論的な運動をしながら、大地震、巨大地震となる。即ち、突如出現する決定論的な大地震や巨大地震の予兆変化は、震源要素時系列のランダム変化に、完全に隠されている。従って、ランダム変化している時系列から、決定論的な変化を導出する、微分操作に代わる新たな数学的手段が必要となる。

ランダムな現象を取り扱う場合、不可能となる微分操作を避けるために、そのランダムな統計分布法則と微分法則を上手に組み合わせた確立微分方程式もあるが、その統計分法則に適合した物理、経済現象しか記述できない。物理現象では、確率過程と微分とを現象論的に結びつけた拡散の偏微分方程式[24]、ランジュバン方程式[24]、ランダムで微分不可能な現象の微分操作を、巧みに回避した伊藤の確立微分方程式[25]、金融工学では、伊藤の補題を発展させたブラック-ショールズ方程式[25]等がある。しかし、これら確立微分方程式は、予兆の性質から、予兆の運動方程式として使用できない。そこで、武田は、「物理的ウエーブレットによるリアルタイム信号処理手法」を開発し [14, 16 - 22]、その手法に証明も与えた [14, 16]。

物理的ウエーブレットは、対象とする信号（時系列）と相関を取り、変位、速度、加速度を検出する。速度、加速度を相関から検出する時、ウエーブレットの形状にマッチする要素を時系列から切り取り、切り取ったサンプルの平均（加算）とサンプル間の差分操作をする。加算操作は、サンプル内の小さな凸凹をスムースにするローパスフィルター機能を持ち、それらサンプル間の差分操作は、スムースにしたサンプル間の大きな凸凹を強調するハイパスフィルター機能を持つ。従って、速度と加速度の検出時、バンドパスフィルターの機能が働いているので、様々な周波数を持って変化（運動）する予兆の情報源から、決定論的に変化する予兆の運動を選択的に抽出できる。

物理的ウエーブレットで観察したCQKとCQT

又、物理的ウエーブレットで観測した図９aと図９ｂのCQKとCQT予兆のイラストが、図９ｃである。

略2sからなる短い固有な周期(時間的な尺度)を持った2種類のA(INT,t)とA(DEP,t)とA(MAG,t)との振幅及び位相関係CQKとCQTが、大地震発生の時刻を定量化する。これら発生時刻は、配列インデックス(地震の発生個数つまりイベント数)のtなので、tと平均的な地震の発生間隔時間との積が、実時間となる。従って、上記、大地震発生の２種類のCQKとCQTの予兆(自然法則)は、2種類の大地震の予知に利用できる。２ｓの値は、中国・四国・近畿では、60～70イベントとなる。１イベントは、単位時間の１でもある。

変位D(c,t)に作用する加速度A(c,t)

ランダム変化する各震源要素ｃ（ｃ＝INT,DEP,MAG）の時系列ｄ（ｃ、ｍ）から、物理的ウエーブレットを用いて検出したスムースな変位D(c,t)は、周期変動しているので、その変位に作用する力は、次の運動方程式で与えられる。

CQKのメカニズム

図10の左側の模式図のＭ7.2の兵庫県南部地震等のCQK予兆検出時、地殻表面から深い個所で、M4地震が多発している。D(DEP,t)、D(INT,t)、D(MAG,t)は周期変動しているので、その半周期後、CQK予兆検出時の地震発生の状態から反転し、地殻表面から浅い個所で、M3.8地震が、時々発生している状態となる。深い個所から浅い個所への反転直後に、CQK予兆の大地震が、発生するので、この反転に伴う震源の深さD(DEP,t)の変化量に相当する応力変化が、CQK予兆の大地震の断層運動を起こす地殻の応力変化を誘発する。

震源の深さD(DEP,t)の変化量をΔD(DEP,t)とすると、その変化の方向は、■の破線矢印が示す深い方から浅い方向の上向きとなる。その変化量ΔD(DEP,t)を発生させる力ΔF(DEP,t)との関係は、運動の第二法則を記述する（数式１）の変分Δを取った式が、ΔF(ｃ,t)＝-KｃΔD(ｃ,t)となるので、変化量ΔD(DEP,t)に比例した力ΔF(DEP,t)は、ΔD(DEP,t)が変化を生じる方向と逆方向に作用する。従って、CQK型のΔF(DEP,t)の方向は、●の破線矢印で示した浅い方から深い方向の下向きとなる。地殻内では、地震発生の変化で生じたΔF(DEP,t)を打ち消す方向、即ち、●の破線矢印で示した上向きの方向に、ΔD(DEP,t)の発生個所より浅い所で、反作用的な応力変化が誘発されると推論される。

その反作用的な応力変化が浅い所の断層に作用し、せん断応力が断層の静止摩擦応力を上回れば、特大フォントサイズのX印で表示したCQK型のM7.2大地震が発生する事になる。せん断応力は、変化量ΔD(DEP,t)を起こした力ΔF(DEP,t)から誘発されたので、ΔD(DEP,t)と略等しい幅W kmを持った断層を動かす事ができると推論される。実際、Ｍ7.2の兵庫県南部地震の変化量ΔD(DEP,t)=20kmは、[26]に報告されている断層幅W=20kmと一致しているので、上記推論は正しい。

CQTのメカニズム

CQT型の大地震(M7.2の鳥取県西部地震等)の場合は、図10の右側の模式図で、次の状況を示している。大地震のCQT予兆検出時、地殻表面から浅い個所で、M4地震が時々発生している。D(DEP,t)、D(INT,t)、D(MAG,t)は周期変動しているので、その半周期後、CQT予兆検出時の地震発生の状態から反転し、深いい個所で、M3.8地震が、多発している状態となる。

この反転直後に、CQT予兆の大地震が、発生する。反転時、CQK予兆の大地震の場合と同様に、D(DEP,t)の変化量をΔD(DEP,t)とすると、その変化の方向は、■の破線矢印で示した下向き方向となる。

ニュートンの運動の第二法則から、●の破線矢印で示した逆向き（上向き）の力ΔF(DEP,t)が、発生し、このΔF(DEP,t)を打ち消す方向、即ち、ΔD(DEP,t)の発生個所より浅い所で、●の破線矢印で示した下向きの反作用的な応力変化が誘発されると推論される。この応力変化が幅W kmの断層に作用し、そのせん断応力が、断層の静止摩擦応力を上回り、大地震を発生させる断層運動が生じたと推論される。M7.2の鳥取県西部地震の場合、ΔD(DEP,t)=15kmとなり、[27]に報告されている推定断層幅、W=17kmと略一致しているので、推論は正しい。

断層幅Wの予測

兵庫県南部地震(1995-1-17、CQK予兆タイプでＭ7.2)、山口県東部地震(1997-6-25、CQT予兆タイプでM6.6)、鳥取県西部地震(2000-10-06、CQTタイプでＭ7.2)、中越地震(2004-10-23、CQTタイプでM6.8)等の大地震の断層形状(長さLと幅W)は、[26-29]によると、大地震の余震分布や地震波観測に基づく断層運動のモデル等から推定されている。これら大地震の推定断層幅Wと、大地震発生前に観測される、D(DEP,t)の変化量ΔD(DEP,t)とを比較すると、山口県東部地震を除き、WとΔD(DEP,t)とが、略、同じ値になる。従って、変化量ΔD(DEP,t)を断層幅Wとする事が出来る。

マグニチュードの予測

日本で観測されたマグニチュードが6≦M≦8.5の地震にたいし、断層の長さＬと幅Ｗの間には、Ｌ≒２Ｗの経験則があり、断層の長さLかＷを用いると、Utsuの経験則[30]から、地震のマグニチュードMは、次式で与えられる。

従って、断層幅Wが予測できると、数式（４）から、大地震や巨大地震のマグニ大チュードの予測が、可能となる。又、GPS観測等で、地殻の臨界状態の広がりをLとして検出できれば、数式（３）からマグニチュードを予知できる。数2の適用範囲を、マグニチュード９まで、拡大して、GPSが捉えた2009年12月8日頃から始まった、東北地方の東海岸、西海岸の異常膨張（東で約１ｍｍ、西で約３ｍｍ）と、太平洋プレートの西方向への異常加速度運動のピークが2010年の12月22日に到達し、巨大地震が、何時発生しても不思議でない時期を迎えたのは、2011年2月の始めであった。この地殻の応力の臨界状態の広がりは、約L= 500 kmに到達していたので、数式（３）から、M9巨大地震を予知できていた [10, 14, 31]。この概要は、予知の節にある。

使用してきたマグニチュードは、気象庁マグニチュードであるが、断層形状のパラメータを用い次式で定義されているモーメントマグニチュード[32]もある。MKS単位で、数式（５）で与えられる。ここで、Ｍ０は地震モーメントで、MKS単位で、数式（６）で定義されている。

ここで、μは、断層を含む地殻の剛性率，Ｄは、断層のすべり量、Ｓは、断層の面積である。Ｓは断層の幅Ｗ(km)と断層の長さＬ(km)との積(Ｓ＝Ｗ・Ｌ)で与えられる。

発生時刻の予測

地震発生の2次の変化率である加速度A(c,t)を、数式（1）の時系列[c]から、図８ｂの加速度検出ウエーブレットを用いて検出する。この時、加速度A(c,t)は、各震源要素間に共通な略2sの短い固有な周期(時間的な尺度)を持って変動するが、大地震発生直前には、通常の地震発生とは異なる2種類のA(INT,t)とA(DEP,t)とA(MAG,t)との振幅及び位相関係が成立する。この２つの特殊な関係が、図９ｃに表示した大地震発生のCQK及びCQT予兆であった。この図で、大地震が発生した時刻は、それら予兆を検出した時刻ta1のA(INT,ta1)もしくはA(DEP,ta1)の振幅のピークが、半周期後に、反転し、逆のピークに到達した時刻ta2である。加速度が、この逆のピークに到達する大地震発生時刻ta2の予測は、次の加速度の周期振動の仮定と方法に基づく。

加速度が、ピークに到達する時刻ta2を正確に予測するには、その変位に作用する加速度A(c,t)間に成立する数式（２）の運動の第二法則を利用する[14]。その運動法則を、図９ｄに表示する。図９ｃと同様に、図９ｄの横軸は、時間t、縦軸は、変位D(c,t)、加速度A(c,t)で、上向きが負、下向きが正の方向となる。図８ｂの加速度検出ウエーブレットの差分間隔時間は、sなので、図９ｄの遅れ時間は、ｓとなる。この時、図９ｄの各時刻は、次の関係を持つ。

図９ｃで、震源要素ｃをINTした大地震発生時刻ta2は、のCQT予兆の大地震が発生する時刻に対応する。時刻ta2の加速度A(INT,ta2)は、変位D(INT,ta2)に作用し、変位D(INT,ta2)は、その振動の山(負の方向のピーク)に在る。図９ｃのCQK予兆の大地震発生の場合は、大地震発生時刻ta2で、図９ｄのA(c,ta2)とD(c,ta2)の位相関係が、それぞれ反転する。

加速度A(INT,t)が時刻tx1の時点で、未だ到達していない振幅の谷(正の方向のピーク)となる時刻ta2を予測する事は、変位D(INT,t)が、確実に負の方向のピークを過ぎた時刻のtx2で、変位D(INT,t)が、負の方向のピークに在った時刻ta2を抽出する事と、等しくなる。従って、「加速度A(INT,t)が、正の方向のピーク値に今から到達する時刻ta2を予測する。」事は、「変位D(INT,t)が、負の方向のピーク値に既に到達した時刻ta2を抽出する。」事になる。加速度A(INT,t)が正の方向のピーク値に到達する時刻は、変位D(INT,t)が、負の方向のピーク値に既に到達した時刻ta2を用いて、時刻tx1から、(ta2-tx1)イベント後に、大地震が発生すると予測できる。変位D(INT,t)は、時刻tx2から更に(ta2-tx1)イベント進んだ時刻ta3で大地震の発生を、観測する事になる[14]。

詳細は省略するが、数式（２）が成立する周波数領域は、図８ｂの変位検出と加速度検出ウエーブレットを構成するΔt＝2ｗ+1と差分間隔ｓを任意選択して与えられる。差分間隔ｓがΔｔより大の時、変位D(INT,t)の振動の周期は、略1/(2w+1)以下の低い周波数領域内で変動し、その2次の変化率を与える加速度A(c,t)は、更に低い周波数の1/(2s)を中心としたバンド幅内で変位D(INT,t)に追従して変動する。従って、加速度A(c,t)の正と負の方向の振幅値のピークに到達する時刻は、差分間隔の時間ｓだけ先に進んだ変位D(c,t)の負と正の方向の振幅値のピークに到達した観測時刻から予測できる[14] 。

加速度A(DEP,t)とA(INT,t)の波形の反転が、図９ｃに示したCQKとCQT様に、略、完全な反転とならない場合、地震発生日は、図９ｃのA(INT,t)が負のピーク値をとる時刻ta2ではなく、A(DEP,t)が、時刻ta2の正のピーク値から更に半周期進んだ負のピーク値を取る時刻となる。その時刻は、図９ｄのA(ｃ,t)とD(ｃ,t)で震源要素ｃをDEPとした関係図を用いると、時刻ta3となる。この発生時刻のta2からta3への遅延は、上記大地震発生のCQK型の物理モデルによると、時刻ta1からta2の変化量ΔD(DEP,t)で生じるΔF(DEP,t)は、時刻ta2で今にも発生しそうな大地震の断層に作用するせん断応力を誘発する。しかし、そのせん断応力は、変化量ΔD(DEP,t)で生じるとされたΔF(DEP,t)よりも少ない量となり、変化量ΔD(DEP,t)に相当する断層幅を持った断層の静止摩擦応力より小さくなる。従って、そのCQK大地震は、時刻ta2で発生しない。時刻ta2からta3までの変化量ΔD(DEP,t)で生じたΔF(DEP,t)により、誘発されたせん断応力が更に加わると、断層に作用するせん断応力は、断層面の静止摩擦応力より大きくなり、そのCQK大地震が時刻ta3で発生する[14]。

ただし、この場合でも、時刻ta1からta2までの変化量ΔD(DEP,t)が、断層幅Wに略等しくなる。従って、断層幅Wを持った断層に作用するせん断応力を生み出す源となるΔF(DEP,t)を発生させる物理モデルは、CQKとCQT予兆の加速度A(DEP,t)とA(INT,t)の波形の反転が、図９ｃに図示した理想的なCQKとCQT予兆の反転と異なる場合、大地震発生時刻の予測を可能とする[14]。

これら予測した発生時刻ｔは、最新の時刻ｍから、ｗだけ遅れている。時刻mは、配列インデックス(地震の発生個数つまりイベント数)なので、ｍと平均的な地震の発生間隔時間との積が、実時間の大地震発生予測時刻となる。

震源の予測

断層幅Wを持った断層に作用するせん断応力を生み出す源となるΔF(DEP,t)を発生させる物理モデルは、任意選択した領域内の震源の予測を、加速度を用いたCQKもしくはCQT予兆検出時刻ｔa１から大地震の発生予測時刻ta2までの変位D(LAT,ｔ)とD(LON,ｔ)とD(DEP,ｔ)とを、加速度よりｓだけ進んだ変位の発生時刻ta2＋sかta3＋sまで線形補間して得る[14]。

予兆と予知、歪エネルギーの蓄積と解放サイクル（臨界サイクル）、地殻変動

地震発生は仮想粒子の出現